عن جد... شو هاظي الطنبولوجيا؟ و كيف يمكن لأي إنسان أن لا يحب
            الطنبولوجيا؟

            ما يدفعني لطرح هذا التساؤل هو أن موسى كتب:
            أكره الطنبولجيا

            معقول يا جماعة؟ عن جد يعني هل هذا معقول؟

            الطبولوجيا هي، بالإضافة لكونها أجمل العلوم الرياضية، هي من أبسط ما
            يكون، و سوف سأحاول في هذا الشريط أن سوف سأشرح ماهيتها. و منه تحذير و
            تنبيه:

            لفهم ما يتبع في هذا الشريط فأنتم بحاجة لمستوى الصف التاسع في سوريا،
            يعني "البروفيل"، و أفضل منه أن تمتلكوا مستوى الباكالوريا (الثانوية
            العامة) العلمية، لكن هذا ليس ضروريا...

            يعني أنا أفترض أن قارئ هذا الشريط يفهم المقصود من كلمة "مجموعة" و
            "أجزاء مجموعة" و "إجتماع أو تقاطع أو فرق مجموعات" و "المجموعة
            الخالية" و إلخ من مبادئ نظرية المجموعات.

            فمن كان يجهل ذلك فأنا أدعوه ألا يتابع، و أما من كان يعلم ذلك فأنا
            أدعوه أن يتفضل بالمتابعة كي يشاركني عشقي للطبولوجيا، إن شاء الله (و
            هو كائن ذو طبولوجيات متعددة).

            فما هي الطنبولوجيا؟

            طيب لتكن مجموعة ما... مثلا مجموعة الأعداد الحقيقية...

            طيب و لتكن مجموعة أجزائها... يعني مجموعة المجموعات المحتواة ضمنها...
            (مثال عن ذلك فيما يخص مجموعة الأعداد الحقيقية، فمن بين أجزائها نجد:
            المجموعة {0}، المجال المغلق [0، 1]، المجال المفتوح مع نفس القيمتين،
            و إلخ...)

            مش مهم...

            لنأخذ شوية شباب من أجزاء مجموعتنا إياها، يعني، و بصيغة رياضية دقيقة:
            لتكن مجموعة جزئية من مجموعة أجزاء المجموعة الكلية...

            بس يعني إذا أزعجتكم الصيغة إياها فيمكننا أن نقول: لنأخذ كوشة مجموعات
            محتواة في مجموعتنا الأساسية -يعني مجموعة مجموعات، يعني مجموعة
            أجزاء...

            و نشترط في هذه الأجزاء شروطا أربعة لعن الله الثلاثة، و هي ما يلي...

            1- المجموعة الخالية تنتمي إليها (أصلا هذا شرط تافه: إن لم يتحقق
            فيكفينا أن نقول و بكل وقاحة: "و نضيف إليها المجموعة الخالية")

            2- المجموعة الكلية تنتمي إليها (أصلا هذا شرط تافه إلخ كما سبق
أعلاه).

            3- إجتماع أي كمية منها ينتمي إليها (أصلا هذا شرط تافه إذ يكفينا أن
            نقول أننا نأخذ هذه الكوشة مجموعات و كل اجتماعاتها).

            4- تقاطع أي عدد منته من عناصرها ينتمي إليها.

            في الحقيقة... من بين هذه الشروط الأربعة هناك شرط واحد صعب (يعني:
            مهم) و هو الشرط الرابع.

            و منه التعريف:
            إن تمكنا من اختراع مجموعة أجزاء تحقق شروطنا الأربعة (يعني خصوصا تحقق
            شرطنا الرابع)، فعندها نسمي مجموعة الأجزاء هذه "طبولوجيا"... و
            خلصنا...

            و بالنظر لأن هذه الطبولوجيا موجودة في مجموعة معينة (هي المجموعة
            الكلية) فنحن نسمي المجموعة الكلية "فضاء طبولوجيا" و نقول أنه "فضاء
            طبولوجي مزود بالطبولوجيا إياها"... و خلصنا...

            يعني إن تمكنتم من فهم هذه الشغلات البسيطة فأنتم صرتم تفهمون
            بالطبولوجيا بمقدار فهمي أنا... لا بل و بأفضل بما لا يقاس من فهمي:
            أنتم أصبحتم تفهمون بالطبولوجيا بمقدار فهم أستاذي العظيم، المرحوم د.
            صلاح الأحمد.

            ذلك أن كل ما يتبقى هو الإستنتاجات و الأمثلة... أليسه؟

            و هاكم مثالين...

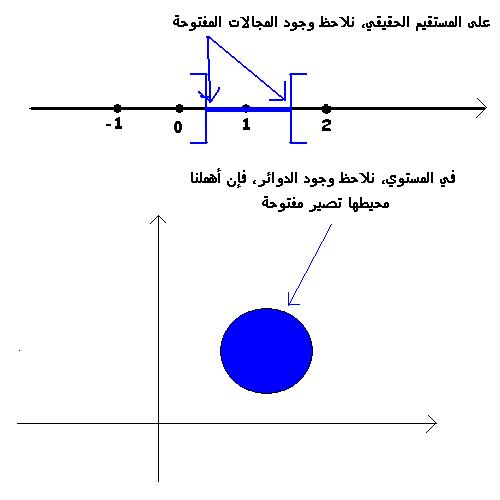
            في الشكل المرفق أنا أوضح مفهوم المجال المفتوح على المستقيم، يعني على
            مستقيم الأعداد الحقيقية، يعني في مجموعة الأعداد الحقيقية "مع
            الطبولوجيا المألوفة".

            يعني:
            إن اعتبرنا مجموعة المجالات المفتوحة + مجموعة اجتماعاتها + المجموعة
            الخالية + المجموعة الكلية ( و هي مجموعة الأعداد الحقيقية) للاحظنا
            أننا نحصل على طبولوجيا تحقق شروطنا الأربعة -لعن الله الثلاثة-
            المطلوبة، و بشكل خاص: هي تحقق شرطنا الرابع، و هو يعني أن تقاطع
            مجالين مفتوحين هو إما أن يكون مجالا مفتوحا (فهو ينتمي لطنبولوجيتنا)
            أو أنه مجموعة خالية (فهو ينتمي أيضا لطنبولوجيتنا... راجع إشارة الجمع
            أعلاه).

            و مفهوم المجال المفتوح على المستقيم يقابله مفهوم الدائرة المفتوحة في
            المستوي: إنها الدائرة حين ننزع محيطها...

            و أما في الفراغ... فالمقابل هو "البرتقالات": البرتقالة هي كرة مغلقة،
            ثم حين نقوم بتقشيرها فهي "كرة مفتوحة"...

            و مجموع البرتقالات المقشرة + إجتماع أي عدد من البرتقالات المقشرة +
            المجموعة الخالية + الفضاء بأكملة، هذا يمثل طبولوجيا نسميها
            "الطبولوجيا التقليدية" أو "الطبولوجيا الإقليدية" (نسبة لسيدنا
            إقليدس)...

            طيب ألم تلاحظوا قديش الطبولوجيا سهلة؟
            يعني كيف يمكن لكم أن لا تحبوها؟

            و يتبع...