قصة الهندسة-7

هاكم أول تكافؤ...

و الآن هاكم ثاني تكافؤ... أو بالأحرى: النصف الأول منه.

للأسف، برهان النصف الثاني من التكافؤ يقتضي برهان عدد لا بأس به من
النظريات، و هو ما سأفعله

برهان التكافؤ بين مسلمة إقليدس و مسلمة ساكيري، الجزء الثاني...

لدينا: مجموع زوايا المثلث قائمتين، المطلوب: برهان مسلمة إقليدس.
صعوبة هذا البرهان تأتي من ضرورة تفسير ما نعنيه بمجوع زوايا المثلث:
هل نقصد هذا المثلث أم ذاك؟ أم أننا ندعي أن كافة المثلثات تتصف بهذه
الخاصية؟ فماذا لو أن مثلثا جاء و قال لنا أنه، يعني هو، ليس مجموع
زواياه قائمتين؟
فيجب أن نجد حالة عامة لكافة المثلثات، فمثلا أن نبرهن: إن وجد مثلث
مجموع زواياه قائمتين، كانت تلك حال اي مثلث آخر... ثم نبرهن التكافؤ
المطلوب.

لأجل ذلك سنقوم ببرهان عدد لا بأس به من نظريات الهندسة المطلقة، أي
الصحيحة تماما مهما كانت الصيغة المعتمدة للمسلمة الخامسة.

توطئة 1. مجموع أي زاويتين في مثلث أقل من قائمتين.
سبق لنا و استنتجناها من النظرية 27 لإقليدس.

توطئة 2. إنشاء هندسي.

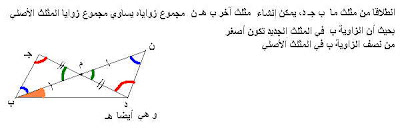
لتكن النقطة م منتصف جـ د. مدد ب م حتى تصل للنقطة ن بحيث: ب م = م ن.
إن كان ب د أطول من ب جـ نصل ن للنقطة د، كما في الشكل، و إلا فنصلها
للنقطة جـ.
استنتج تساوي المثلثين ب م جـ ، م ن د.
استنتج أن مجموع زوايا المثلث ب ن د يساوي مجموع زوايا المثلث ب جـ د.
استنتج أن الزاوية ب في المثلث القديم تساوي مجموع الزاويتين ب و ن في
المثلث الجديد.
استنتج أيضا أن الزاوية ن في المثلث الجديد أكبر من الزاوية ب فيه
(لأنها تقابل أطول الأضلاع ب د).
استنتج أخيرا أن الزاوية ب في المثلث القديم أكبر من ضعف الزاوية ب في
المثلث الجديد، و هو المطلوب.

توطئة 3: مجموع زوايا أي مثلث هو حتما أصغر أو يساوي قائمتين.
البرهان: افترض العكس. افترض أن مجموع زوايا أحد المثلثات كان يساوي
قائمتين مضافا إليهما مقدار ما، نسميه ف.
باستخدام الإنشاء الهندسي أعلاه، و بتكراره عددا كافيا من المرات، يمكن
لنا أن نحصل على مثلث تكون فيه الزاوية ب أصغر من ف، فيكون مجموع
الزاويتين الأخريين أكبر من قائمتين، و هذا مناقض للتوطئة 1.
و هو المطلوب.

هذه التوطئة تثبت لنا أن هندسة ريمان خاطئة: لا يمكن أن يكون مجموع
زوايا المثلث أكبر من قائمتين...
بالمقابل، و إن قبلنا التخلي عن المسلمة السادسة أيضا... فعندها لكل
حادث حديث...

توطئة 4: إن كان مجموع زوايا مثلث ما قائمتين، ثم أنزلنا خطا من أحد
رؤوسه على الضلع المقابل، لحصلنا على مثلثين مجموع زوايا كل منهما
قائمتين بالضبط.
السبب: لا يمكن لمجموع زوايا أحدهما أن يكون أصغر من قائمتين لأن ذلك
يجعل مجموع زوايا الآخر أكبر من قائمتين.

توطئة 5:
لئن وجد مثلث ب جـ د مجموع زواياه يساوي قائمتين، لوجد مثلث قائم
متساوي الساقين مجموع زواياه يساوي قائمتين.
ليكن المثلث ب جـ د مجموع زواياه يساوي قائمتين كما في الشكل، ليكن ب
جـ هو أقصر أضلاعه...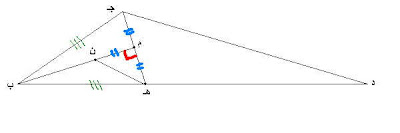

خذ على ب د مسافة مساوية للضلع ب جـ، و لتكن ب هـ. ارسم الخط جـ هـ.
لتكن م منتصفه. ارسم ب م. برهن تساوي ب م جـ مع ب م هـ. استنتج أن
الزاوية الرسومة بالأحمر قائمة. ليكن الضلع القائم ب م أطول من م هـ ،
خذ عليه نقطة ن بحيث ن م = م هـ
نحصل على ن م هـ مثلث قائم متساوي الساقين.
استخدم التوطئة 4 و كرر استخدامها حتى تصل للبرهان على أن مجموع زواياه
يساوي مجموع زوايا المثلث الأصلي، اي قائمتين.

توطئة 6.
إن وجد مثلث قائم متساوي الساقين و مجموع زواياه يساوي قائمتين،
فيمكننا انطلاقا منه إنشاء مثلث أكبر منه بالقدر الذي نرغب به بحيث
يكون المثلث الجديد قائما متساوي الساقين و يكون مجموع زواياه قائمتين.
البرهان: ضع نسخا من هذا المثلث بجانب بعضها.

توطئة 7.
إن وجد مثلث قائم متساوي الساقين و مجموع زواياه قائمتين، فمجموع زوايا
اي مثلث قائم أصغر منه هو قائمتين.
البرهان: طابق الزاويتين القائمتين و استخدم التوطئة 4 عددا من المرات
(مرتين) حتى تحصل على النتيجة المطلوبة.

توطئة 8.
إن وجد مثلث مجموع زواياه يساوي قائمتين، كان مجموع زوايا أي مثلث آخر
يساوي قائمتين.
البرهان:
استخدم المثلث الأول (مجموع زواياه قائمتين) و التوطئتين 5 و 6 للحصول
على مثلث قائم متساوي الساقين أكبر من المثلث الثاني.
من أحد رؤوس المثلث الثاني ارسم عمودا يسقط على الضلع المقابل (في حالة
مثلث قائم أو منفرج الزاوية، اختر الراس القائم أو المنفرج). فتحصل على
مثلثين قائمين أصغر من المثلث الأصلي.
استخدم التوطئة 8 للبرهان أن مجموع زوايا كل منهما قائمتين. استنتج أن
مجموع زوايا المثلث الثاني قائمتين.

هذه التوطئة تسمح لنا أن نكتب:
كافة المثلثات تتصف بما يلي:
فإما أن مجموع زوايا كل منها يساوي قائمتين بالضبط،
أو أن مجموع زوايا كل منها أصغر تماما من قائمتين.

توطئة 9.
من نقطة ب خارج مستقيم ق، يمكن لنا أن ننشئ مثلثا ب جـ د بحيث تقع جـ د
على ق و تكون الزاوية جـ أصغر من اي قيمة معطاة سلفا...
البرهان: ارسم العمود ب د النازل من ب على ق. خذ مسافة ما على المستقيم
و ارسم المائل ب هـ. خذ مسافة هـ ن = ب هـ. ادرس المثلث متساوي الساقين
ب هـ ن، استنتج أن الزاوية ب هـ ن أصغر من نصف ب ن د. كرر هذا التنصيف
حتى تصل لزاوية ب جـ د أصغر من القيمة المطلوبة.

نظرية:
إذا كان مجموع زوايا المثلث يساوي قائمتين، فمن نقطة خارج مستقيم يمكن
إنشاء مواز واحد لهذا المستقيم.

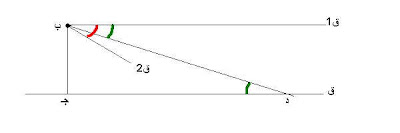
لتكن النقطة ب خارج المثلث ق. نرسم العمود ب جـ. ثم نرسم ق1 عموديا
عليه. اعتمادا على النظرية 27 لإقليدس، فهو مواز للمستقيم ق.
لنفترض جدلا وجود ق2 مواز آخر للمستقيم ق. فهو مختلف عن ق1، فيصنع معه
زاوية ما، نسميها يه (مرسومة بالأحمر). من التوطئة 9 نرسم المائل ب د
بحيث تكون ب د جـ أصغر من يه. بما أن مجموع زوايا ب د جـ هو قائمتين،
نستنتج تساوي الزوايا المرسومة بالأخضر. نستنتج أيضا أن يه أكبر من
الزاوية بين ق2 و ق1، فنستنتج أن ق2 يقع ضمن المثلث ب د جـ، فهو إذن
سيقطع المستقيم ق في نقطة أقرب من د.
و هذا مناقض للفرض، فنستنتج استحالة وجود ق2، و هو المطلوب...

إذن: مسلمة ساكيري تعطي مسلمة بلايفير... و نحن نعلم أن هذه تعطي مسلمة
إقليدس، فنستنتج أن مسلمة ساكيري تعطي مسلمة إقليدس...

سأعود لأضيف برهانا أخيرا أو اثنين على التكافؤ بين صيغ المسلمة
الخامسة...
فلي عودة.